分割回文串

给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。

返回 s 所有可能的分割方案。

示例

输入: “aab”

输出: [ [ “aa” , “b” ] , [ “a” , “a” , “b” ] ]

思路

对于这个题，首先需要考虑怎么切，然后还需要考虑判断回文串。

首先是怎么切，可以分层切割字符串，第一次切成两部分，第二次将第一次切的后半部分切成两部分……最后需要切的部分为空字符串就结束，这样可以获得所有的切法，也就是这样：

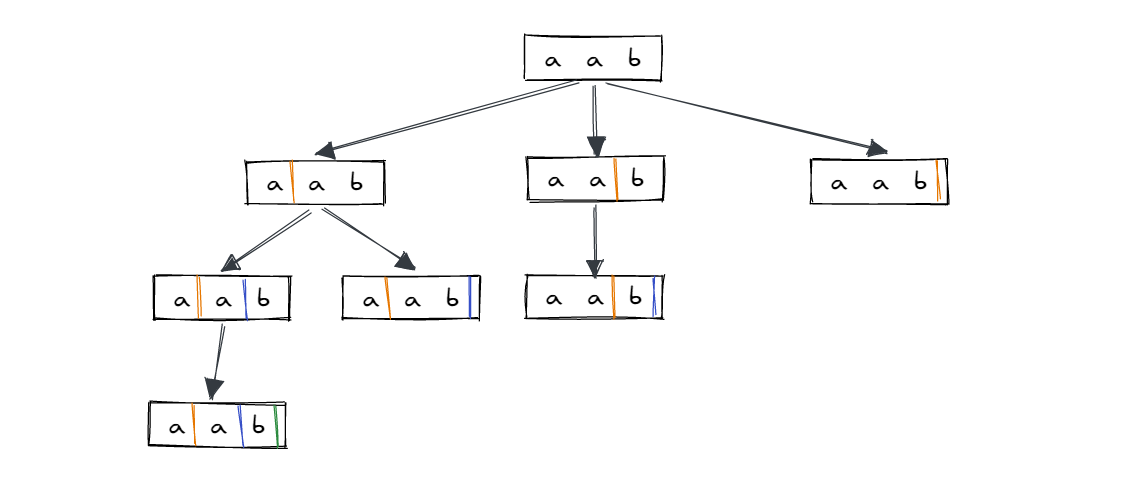
虽然切割好了，但是我们是要将字符串切为回文串，所以在每次切割时判断切下来的串是否是回文串，如果不是就终止本次切割。

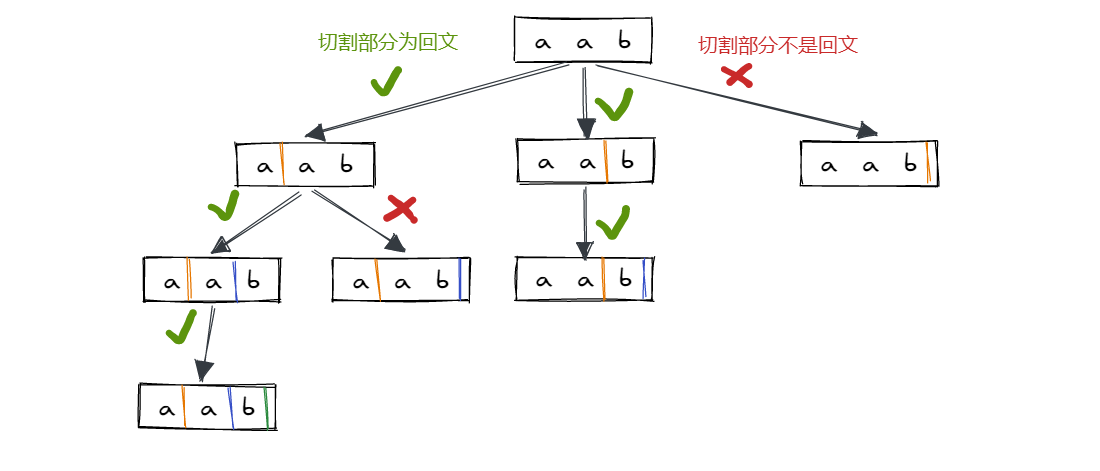
这样解法就比较清楚了，可以使用回溯的方法来解这道题：

• 递归函数参数：本次要切割的字符串s，存放结果的列表ans，切割后回文子串列表cs
• 终止条件：要切割的字符串为空串
• 单层逻辑：依次从1位置开始到s.length()将串切割为两部分，如果前半部分是回文串，则将前半部分加入cs，并且继续切割后半部分。如果前半部分不是回文串，则跳到下一个位置切割。

实现代码

class Solution {
    public List<List<String>> partition(String s) {
        List<List<String>> ans=new ArrayList<>();
        List<String> cs=new ArrayList<>();
        backtracking(s,ans,cs);
        return ans;
    }

    public void backtracking(String s,List<List<String>> ans,List<String> cs) {
        if("".equals(s)) {
            ans.add(new ArrayList<>(cs));
            return;
        }
        for(int i=0;i<s.length();i++) {
            String part=s.substring(0,i+1);
            if(!isPalindromic(part))
                continue;
            cs.add(part);
            backtracking(s.substring(i+1),ans,cs);
            cs.remove(cs.size()-1);
        }
    }

    // 判断是否是回文串
    public boolean isPalindromic(String s) {
        for(int i=0;i<s.length()/2;i++) {
            if(s.charAt(i)!=s.charAt(s.length()-i-1))
                return false;
        }
        return true;
    }

}

上面的使用了许多substring方法，也可以用下标来表示切割的字符串，因为每次都是切割为两部分，只需要用一个startIndex来表示切割的位置就好了。

class Solution {
    public List<List<String>> partition(String s) {
        List<List<String>> ans=new ArrayList<>();
        List<String> cs=new ArrayList<>();
        backtracking(s,0,ans,cs);
        return ans;
    }

    public void backtracking(String s,int startIndex,List<List<String>> ans,List<String> cs) {
        if(startIndex==s.length()) {
            ans.add(new ArrayList<>(cs));
            return;
        }
        for(int i=startIndex;i<s.length();i++) {
            if(!isPalindromic(s,startIndex,i+1))
                continue;
            String part=s.substring(startIndex,i+1);
            cs.add(part);
            backtracking(s,i+1,ans,cs);
            cs.remove(cs.size()-1);
        }
    }
	
    // 判断是否是回文串
    public boolean isPalindromic(String s,int start,int end) {
        for(int i=start;i<(end-start)/2+start;i++) {
            if(s.charAt(i)!=s.charAt(start+end-1-i))
                return false;
        }
        return true;
    }

}