背包问题
01背包
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
示例
背包最大重量为4。
物品为:
| 物品 | 重量 | 价值 |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
问背包能背的物品最大价值是多少?
输出:35
思路1
使用二维数组dp,dp[i][j]表示从下标为0-i的物品任意取,放进容量为j的背包的最大价值总和。
如何递推?因为是向背包中装物品,所以对于dp[i][j]来说就是装不装物品i的区别:
- 不装物品i:既然不装物品i,即背包容量为j,里面不放物品i的最大价值,那么
dp[i][j]就是dp[i-1][j] - 装物品i:装了物品i,就需要由背包容量为
j-weight[i]里面不放物品i的最大价值来推出,即dp[i][j]就是dp[i-1][j-weight[i]]+value[i]。
所以可以由以下公式递推:
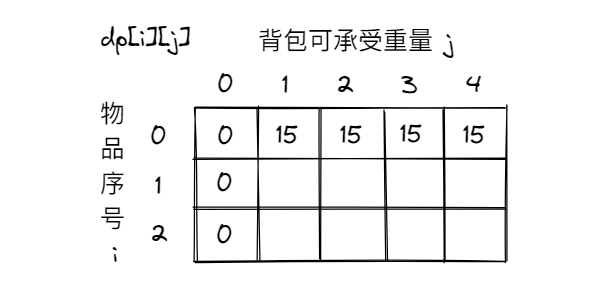
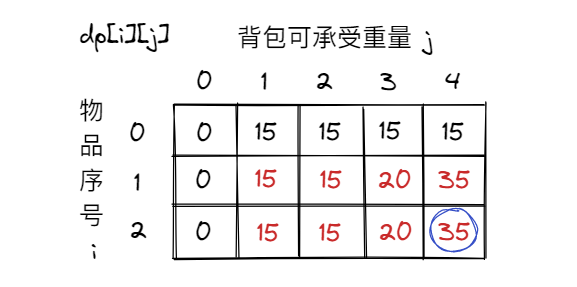
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);对于数组的初始化:首先背包容量为0时,最大价值肯定为0;又因为dp[i]是由dp[i-1]推导的,所以最好将i=0的时候初始化,当j<weight[0]时,背包无法承受物品0,所以最大价值为0,j>=weight[0]时,背包可以承受物品0,所以最大价值为物品0的价值。
可将dp初始化如下:
从递推公式可以看出无论是先遍历物品还是先遍历背包容量都是可以的
代码实现1
class Solution {
public int backpack(int[] weight,int[] value,int packWeight) {
int m=weight.length;
int n=packWeight+1;
int[][] dp=new int[m][packWeight+1];
//初始化
for(int j=weight[0];j<n;j++) {
dp[0][j]=value[0];
}
for(int i=1;i<m;i++) {
for(int j=1;j<n;j++) {
if(j<weight[i]) //物品重量超过背包容量
dp[i][j]=dp[i-1][j];
else
dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);
}
}
return dp[m-1][n-1];
}
}思路2
从使用二维数组的思路来看,递推公式为
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);可以发现如果先将dp[i - 1]那一层拷贝到dp[i]上的话,表达式可以是:
dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);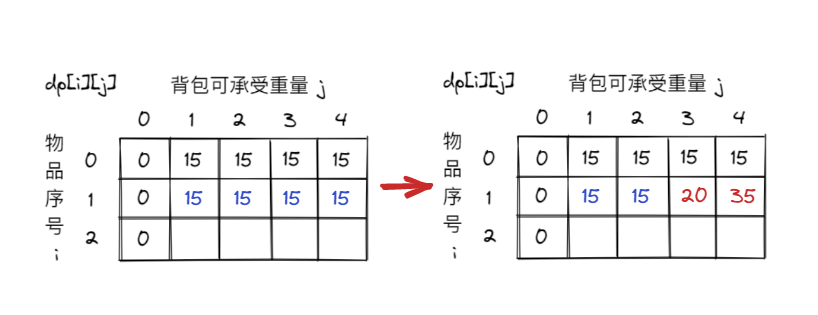
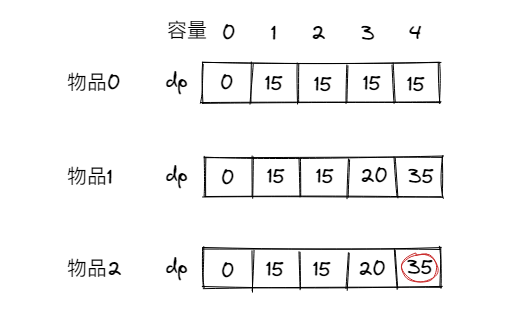
那倒不如直接只用一个一维数组dp[j]了,dp[j]表示容量为j的背包,所背的物品价值可以最大为dp[j]。递推公式为:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);当j=0即容量为0时,最大价值为0,所以可将dp[0]初始化为0。观察递推公式,每次都是取最大的价值并且价值都是正整数,所以应将非0下标也初始化为0。
对于遍历顺序,首先需要倒序遍历容量,因为dp[j]实质上是dp[i][j]拷贝了dp[i-1][j],如果正序遍历,前边添加了物品i算出了新的dp[j],后边容量比前边大肯定也要添加物品i,如果后边的dp[j]是由前边添加了物品i的dp[j]推出的,那么就添加了两次物品i;倒序遍历的话,因为倒序容量是减少的,dp[j]推出时使用的是上一层的结果,也就是dp[i-1][j]。
然后外层遍历必须是物品,因为容量必须倒序遍历,前边的dp[j]全是0,所以如果内层遍历物品,dp[j-weight[i]]永远为0,所以一次容量遍历下来只能添加一个物品。
所以最终的遍历顺序为:
for(int i=0;i<weight.length;i++) {
for(int j=packWeight;j>=0;j--) {
}
}
代码实现2
public int backpack2(int[] weight,int[] value,int packWeight) {
int[] dp=new int[packWeight+1];
for(int i=0;i<weight.length;i++) {
for(int j=packWeight;j>=0;j--) {
if(j>=weight[i])
dp[j]=Math.max(dp[j],dp[j-weight[i]]+value[i]);
}
}
System.out.println(Arrays.toString(dp));
return dp[packWeight];
}完全背包
待续…